Do LLMs put Pineapple on Pizza?

What is the underlying model of the world that is learned by different Language Models? How can we explore these learned representations? The first thing that comes to mind to explore these are embeddings learned by the model. Through embeddings, we can explore the high-dimensional space where entities, concepts, and objects are placed by the model.

As an Italian, I wonder how close pizza and pineapple are in the embedding space of different models. Is this distance greater when comparing it to pizza and ananas (Italian word for pineapple)? Can the model capture this cultural difference and separate the two concepts? Ultimately, which LLMs put pineapple on their pizza?

Innovative Italian torture methodology

Given two embeddings (pizza and pineapple)that represent different entities in the dimensional space, how can you compute the distance between them? The most frequently used metric is cosine similarity, looking at the cosine of the angle between two vectors. Another option is the simpler Euclidean distance between the two vectors. In both cases, we can get a quantitative measure of the distance but not much information about how the embedding space is organized. How are different concepts clustered? What are the entities between the two vectors of interest?

To answer these questions, we can traverse the embedding space going from pizza to pineapple and record the path we took to get there. Specifically, given a corpus of words/entities (food items in this case), we can map them in the embedding space and create a kNN graph connecting the closest k vectors to each item. With this setup, we can navigate the embedding space from one vector (pizza) to the other (pineapple) and record the distance and the entities (i.e. food items) that are traversed to get to the destination.

Cute cat traversing to embedding space to go from Pizza to Pineapple

To do this, we are going to need a few pieces. If you are interested in the source code, you can access it in the GitHub repo for this project. Here we are going to go through it at a high level.

1. CorpusProvider: responsible for returning the dictionary/corpus we want to navigate.

2. Generator: responsible for generating the embedding vector of each entity.

3. GraphConstructor: given the list of embedding vectors for our corpus, we need a way to construct a graph out of it. Here we can use different techniques and ways to compute distance (e.g. kNN with cosine similarity).

4. Traverser: we need something capable of traversing the graph from one node (pizza) to the other (pineapple) and recording the steps to get there.

5. EmbeddingsExplorer: this class puts everything together, generating the corpus, computing the embeddings for it, constructing the graph, and ultimately traversing it.

Let’s put everything together and see which model is best for our pizza-to-pineapple task. First, we generate a corpus of 600 food items appropriate for the challenge in both Italian and English using Claude. Then, we implement different generators for both OpenAI’s text-embedding-3 models and Voyage models (voyage-2 + voyage-2-large).

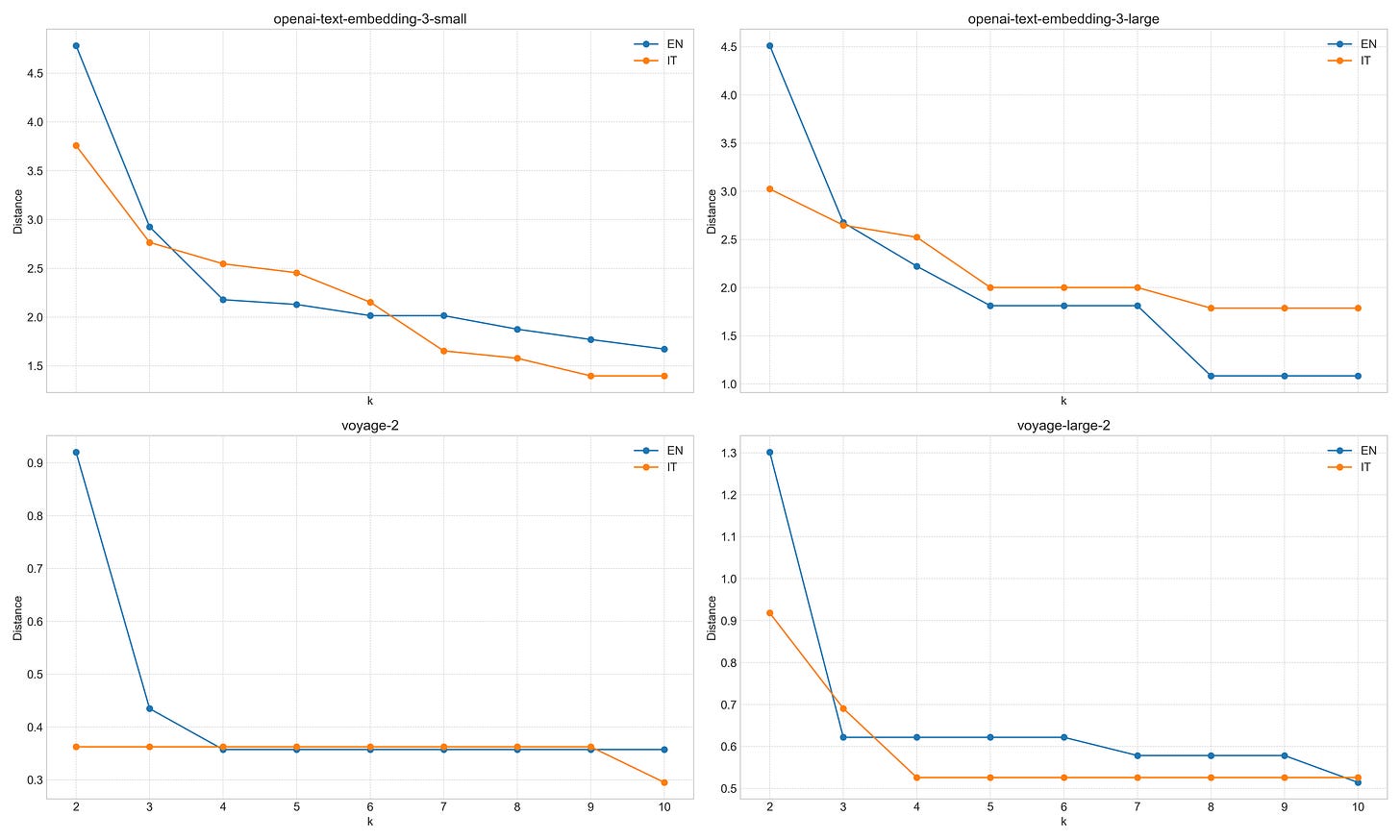
For the first try, I constructed the graph using kNN and cosine similarity as a distance measure. We can also use different values for k, determining how interconnected the graph will be. We expect the distance to be smaller with higher k-values since more routes are available from one node to the other. Sadly, for all the models, we don’t see a greater distance for the embeddings extracted using the Italian vocabulary (see figure below). If we look into some of the paths that were traversed, we get something like this:

Language=EN, k=4
Pizza -> Pepperoni -> Vegan Pepperoni -> Vegan Bacon -> Coconut Bacon -> Coconut -> Pineapple

Language=EN, k=10
Pizza -> Pie -> Pear -> Peach -> Pineapple

Language=IT, k=4
Pizza -> Pasta -> Spaghetti -> Asparagi -> Peperoni -> Peperoncino -> Peperoncino banana -> Banana -> Ananas

Language=IT, k=10
Pizza -> Peperoni -> Peperoncino banana -> Ananas

Note: Peperoni in Italian are vegetables: bell peppers (green/red/yellow). The fact that peperoni is close to Pizza in the “Italian” embedding space probably indicates that the English Pepperoni (Salamino Piccante) is being considered instead.

Distance (y-axis) for different models between pizza and pineapple in English (EN) and Italian (IT) using different K (x-axis) and cosine similarity to construct the graph

For the second try I used Euclidean distance normalized for the vector’s length. The latter allows us to compare models with different embedding sizes and is achieved by dividing the Euclidean distance by the square root of the length of the vectors.

\( d_{\text{normalized}}(\mathbf{u}, \mathbf{v}) = \frac{d(\mathbf{u}, \mathbf{v})}{\sqrt{n}} = \frac{\sqrt{\sum_{i=1}^{n} (u_i - v_i)^2}}{\sqrt{n}} \)

Here are the results of the second set of trials for all 4 models in English and Italian. Sadly, the outcome is not changing much.

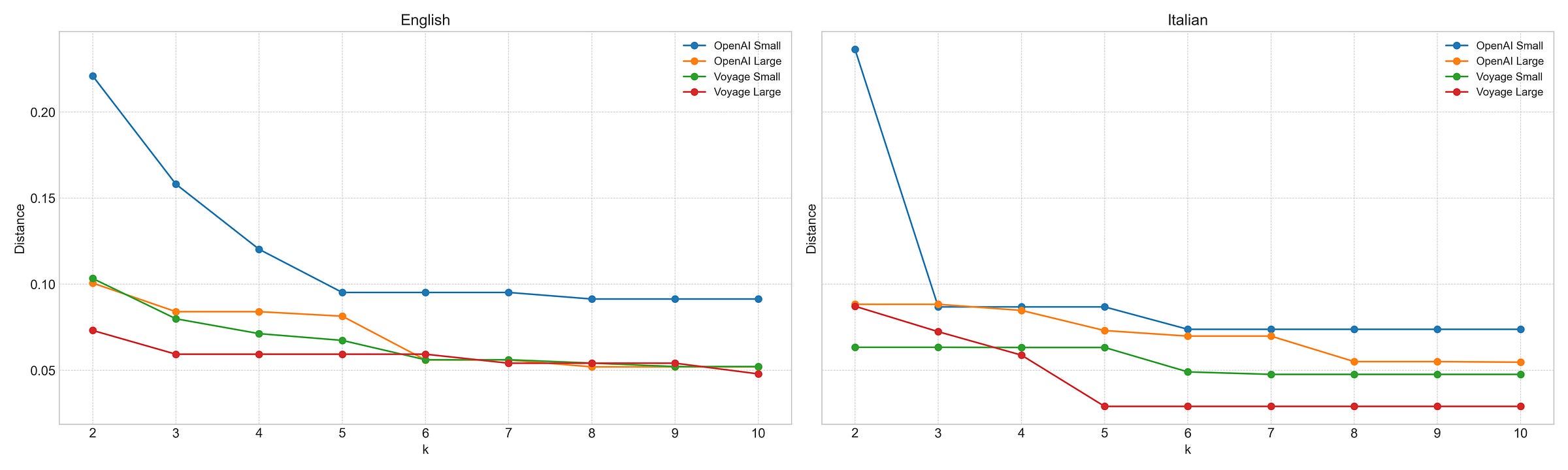
pizza-to-pineapple Euclidean Normalized Distance Comparison for different K (x-axis) and different models to compute embeddings

So, what’s next?

• Performance: Some tasks could be parallelized to improve speed (e.g. when computing embeddings) but the focus was on exploring the idea first.

• Website: What I have in mind is something similar to the Embedding Projector of TensorFlow but designed for traversing embedding spaces with a custom vocabulary, instead of visualizing the embedding space using a 3D space.

• Finetune: construct a loss function that allows to space things apart that we want to be more distant in the space.

Let me know any other secret ingredients that you would like to put on your pizza, I am curious.